在深度学习领域中,神经网络是一种强大的工具,它可以模拟人脑神经元之间的相互作用,实现各种复杂的任务。而激活函数作为神经网络的重要组成部分,对于网络的性能和表征能力起着至关重要的作用。本文将探讨激活函数的重要性以及常用的几种激活函数。
1. 什么是激活函数
激活函数是神经网络中的一个关键组件,它对神经元的输入进行非线性变换,将其转化为输出信号。激活函数的主要作用是引入非线性特性,使神经网络能够更好地拟合非线性函数,从而提高网络的表达能力。
2. 激活函数的重要性
如果神经网络中只使用线性激活函数,那么网络的表达能力将受到限制,无法处理复杂的非线性模式。激活函数的引入能够使网络具备更强的非线性表达能力,从而能够拟合更复杂的问题。
3. 激活函数汇总
3.1 Sigmoid
Sigmoid函数广义上来说,是一类具有S形状曲线的函数统称,例如逻辑Sigmoid函数和双曲正切函数均属于Sigmoid类函数。 但一般情况下提到Sigmoid函数,如果不做特殊说明,特指逻辑Sigmoid函数。 后续文中也将沿用这一习惯。
Sigmoid函数最早由比利时数学家 Pierre François Verhulst 在1838年提出,他在试图通过数学模型描述人口增长的过程中,引入了一种S型曲线函数来表示群体增长的饱和特性,这个函数后来被称为Sigmoid函数。 20世纪50年代到60年代早期,随着感知机模型的发展,Sigmoid函数逐渐开始被应用于机器学习领域。这些早期的研究为后来的机器学习算法和神经网络的发展奠定了基础。
Sigmoid函数定义为:
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]常见的Sigmoid函数图为了凸显函数的特点,Y轴坐标刻度通常与X轴坐标刻度比例不一致。下图中采用一致坐标以展现函数更直观的样子。
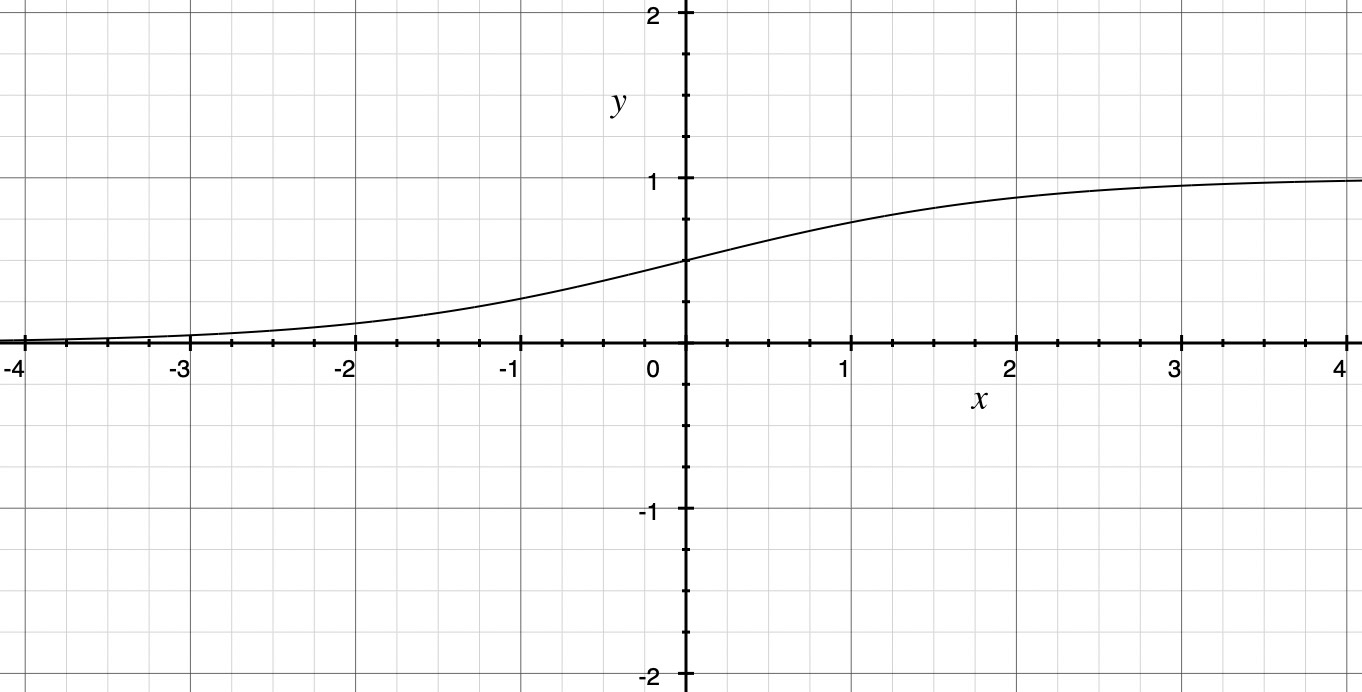
虽然Sigmoid函数非常经典,但是随着深度学习的发展,逐渐暴露出来很多问题:
梯度消失问题:Sigmoid函数的导数在输入较大或较小的情况下接近于零,导致在网络的反向传播过程中梯度逐渐减小,甚至可能趋近于零。这会导致深层网络的训练变得困难,因为较小的梯度会导致参数更新变得缓慢,甚至近乎停止更新。
输出非零中心:Sigmoid函数的输出范围在0到1之间,这导致神经元的输出总是正向的,不以零为中心。这可能导致在网络训练过程中的不对称性,影响网络的学习能力。
计算开销问题:Sigmoid函数的计算开销较大,因为它涉及指数运算。在深度神经网络中,大规模的指数计算会带来额外的计算负担。
基于以上几个原因Sigmoid函数在深度学习领域应用较少,仅在诸如逻辑回归模型等浅层网络中仍有应用。
Sigmoid 总结:
- 别名:Logistic函数, S型函数, 乙状函数,费努瓦函数
- 表达式: \(\sigma(x) = \frac{1}{1 + e^{-x}}\)
- 导数: \(\sigma'(x) = \sigma(x)(1-\sigma(x))\)
- 优点
- 输出范围有限\((0,1)\)
- 连续函数,便于求导
- 缺点
- 梯度消失
- 输出非0均值
- 指数形式,计算时间复杂度高
3.2 Tanh
双曲正切函数的历史发展与指数函数和对数函数的研究相关。早在17世纪,数学家尼科拉斯·梅尔塞尼(Nicolas Mercator)研究了双曲正弦函数和双曲余弦函数,并引入了双曲正切函数作为它们之间的比值。这些函数被称为双曲函数,因为它们与圆锥曲线的双曲线有关。
双曲正切函数定义为:
\[tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]双曲正切函数在形状上与Sigmoid函数相似,与Sigmoid函数相比,双曲正切函数的输出范围更广,包括负数。这使得它在一些情况下更适用,尤其是在处理输入数据的平均值为0的情况下,例如图像处理中对像素值的归一化。
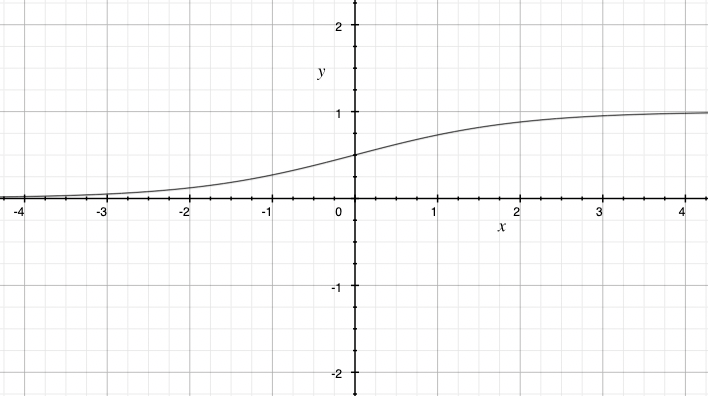
双曲正切函数可以将输入映射到范围\((-1, 1)\)之间,关于原点对称。这一特点很好的解决了Sigmoid函数存在的输出非零中心问题,但除此之外仍然存在梯度消失和指数计算开销大的问题。
Tanh总结:
- 别名:双曲正切函数
- 表达式: \(tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\)
- 导数: \(tanh'(x) = 1-[tanh(x)]^2\)
- 优点
- 输出范围有限\((-1,1)\)
- 输出0均值
- 缺点
- 梯度消失
- 指数形式,计算时间复杂度高
3.3 ReLU
ReLU函数的提出可以追溯到20世纪90年代。一些早期的研究工作提到了类似ReLU函数的激活函数的概念,但当时还没有引起广泛的关注。
ReLU函数真正引起广泛关注和应用的时间是在2010年代。在2011年,Hinton等人在一篇名为《Rectified Linear Units Improve Restricted Boltzmann Machines》的论文中首次提到了ReLU函数,并证明了它在训练深度神经网络中的优势。
ReLU 的定义为:
\[f(x) = max(0, x)\]ReLU函数在输入为负数时输出为0,在输入为正数时输出与输入相等。它的形状是一条折线。
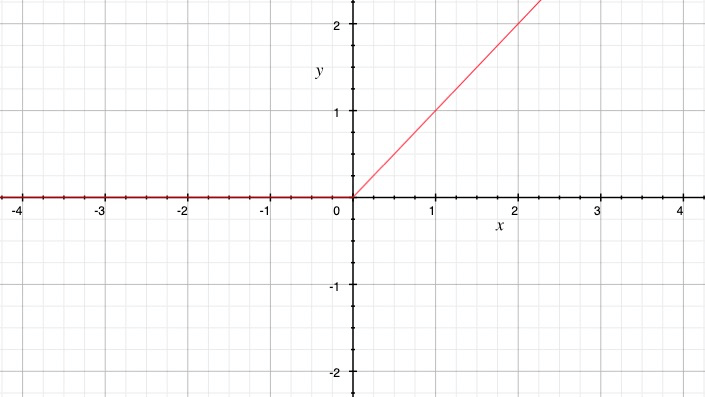
ReLU函数具有许多优点,使其成为深度学习中的首选激活函数之一。它的计算速度非常快,因为它只涉及简单的阈值比较。此外,ReLU函数在训练过程中不会引发梯度消失的问题,并且能够更好地处理稀疏性和非线性特征。这些特性使得ReLU函数在深度学习任务中取得了显著的成功,并成为了许多流行的深度学习架构的默认激活函数。
尽管如此,ReLU仍然存在 Dead ReLU Problem(神经元坏死现象):ReLU在负数区域被kill的现象叫做dead ReLU。在x<0时,梯度为0,这使得ReLU在训练的时很脆弱。
ReLU 总结:
- 别名:整流线型单元,Rectified linear unit
- 表达式: \(f(x) = max(0, x)\)
- 优点
- 使用ReLU的SGD算法的收敛速度比 sigmoid 和 tanh 快
- 在x>0区域上,不会出现梯度饱和、梯度消失的问题
- 计算复杂度低,不需要进行指数运算,只要一个阈值就可以得到激活值
- 缺点
- 输出不是0均值的
- Dead ReLU Problem
- 分段不平滑
3.4 Leaky ReLU
2013年,Andrew L. Maas等人在一篇名为《Rectifier Nonlinearities Improve Neural Network Acoustic Models》的论文中首次提出Leaky ReLU。在该论文中通过实验证明,相对于传统的ReLU函数,Leaky ReLU函数可以进一步改善神经网络在语音识别等任务上的性能。
Leaky ReLU(Leaky Rectified Linear Unit)函数是ReLU函数的一种变体,它在输入为负数时引入了一个小的斜率,通常为0.01。
Leaky ReLU函数的定义:
\[f(x) = max(0.01x, x)\]与ReLU函数相比,Leaky ReLU函数在负数部分引入了一个小的斜率,这使得负数输入的信息不会完全消失。通过引入非零的斜率,Leaky ReLU函数可以在负数部分传递一些梯度,从而缓解神经元死亡现象,增加模型的表达能力。
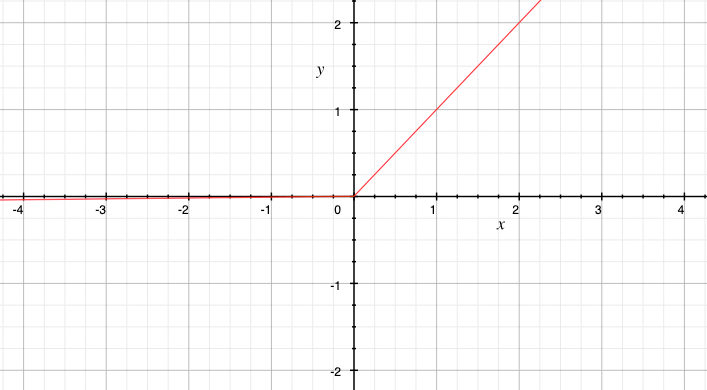
Leaky ReLU函数的引入为神经网络的训练和性能提供了一个有效的改进方案,特别是在处理具有负数输入的情况下。被广泛用于各种深度学习任务中。
Leaky ReLU总结:
- 别名:渗漏线性单元
- 表达式: \(f(x) = max(0.01x, x)\)
- 优点
- 缓解 Dead ReLU Problem
- 缺点
- 输出不是0均值的
- 分段不平滑
- 预定义斜率
3.5 PReLU
2014年,Kaiming He等人在一篇名为《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》 的论文中首次提出PReLU。在这篇论文中,研究人员通过实验证明,相对于传统的ReLU函数和Leaky ReLU函数,PReLU函数可以进一步提升神经网络的表现。
PReLU与Leaky ReLU函数类似,但它不仅引入了一个小的斜率,还允许这个斜率作为可学习的参数进行训练。
PReLU函数的定义:
\[f(x) = max(\alpha x, x)\]其中,\(\alpha\)是一个可学习的参数,可以通过反向传播算法进行优化和调整。
与Leaky ReLU函数不同,PReLU函数不需要事先指定一个固定的斜率。相反,斜率是通过反向传播算法学习得到的。这使得PReLU函数在模型的表示能力和灵活性方面具有一定的优势。通过允许斜率可学习,PReLU函数可以自适应地调整负数输入的传递程度,从而提供更好的模型表达能力。
然而,PReLU函数也引入了更多的参数,增加了模型的复杂性和训练的困难度。
PReLU总结:
- 别名:参数整流线性单元,Parametric Rectified Linear Unit
- 表达式: \(f(x) = max(\alpha x, x)\)
- 优点
- 缓解 Dead ReLU Problem
- 允许斜率可学习。
- 缺点
- 输出不是0均值的
- 分段不平滑
3.6 ELU
2015年,Djork-Arne Clevert等人在一篇名为《Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)》的论文中首次提出ELU。
ELU在负数部分引入了指数函数,具有平滑且非线性的特性。
ELU函数的定义:
\[f(n) = \begin{cases} x, & \text{if }\text{ is x > 0} \\ \alpha(e^x - 1), & \text{if }\text{ is x <= 0} \end{cases}\]其中,\(\alpha\)是一个可调节的超参数,控制ELU函数在负数部分的曲线形状。通常,\(\alpha\)取一个较小的正数,如0.01。
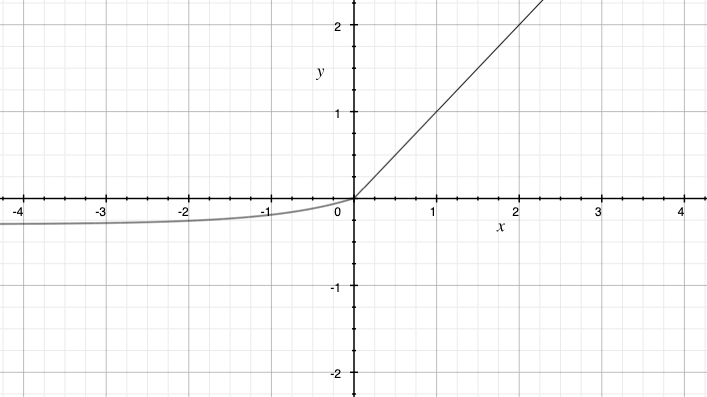
ELU函数的引入主要是为了解决ReLU函数的一些限制,如负数部分的输出为零和梯度消失问题。与ReLU函数相比,ELU函数在负数部分引入了指数函数,使得负数输入的信息能够更好地传递和保留。这有助于减少神经元死亡现象。
- 别名:指数线性单元,Exponential Linear Unit
- 优点
- 输出均值接近0
- 缓解 Dead ReLU Problem
- 缺点
- 指数计算复杂度
3.7 GELU
2016年,Hendrycks和Gimpel在一篇名为《Gaussian Error Linear Units (GELUs)》的论文中首次提出GELU。
GELU定义为:
\[GELU(x) = xP(X ≤ x) = xΦ(x)\]可近似为:
\[\small GELU(x) =0.5x(1 + tanh[2∕π(x + 0.044715x3)])\]GELU函数具有平滑的曲线形状,可以提供更强的非线性表示能力。此外,GELU函数的导数形式也可以被简化,便于计算和反向传播。
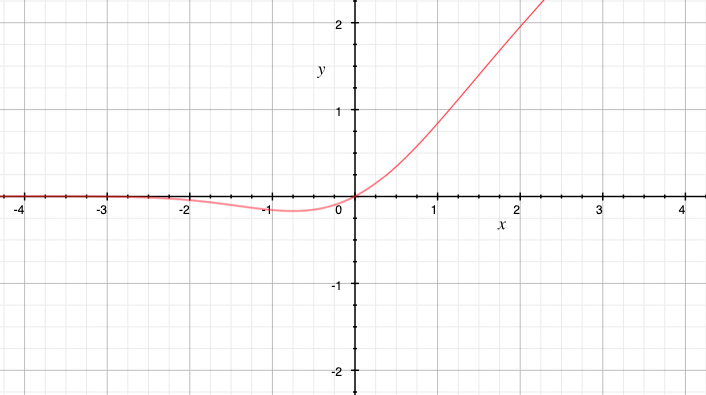
GELU函数在自然语言处理任务中表现出色,尤其在基于Transformer架构的模型中得到广泛应用。它已被证明可以提升机器翻译、语言模型和文本分类等任务的性能。
- 别名:高斯误差线性单元,Gaussian Error Linear Unit
- 优点
- 平滑
- 缺点
- 计算复杂度稍高