在深度学习发展的早期,人们根据二维,三维空间的经验印象,会担心优化算法陷入局部最优解。但随着深度学习领域的研究越来越深,人们对局部最优问题的看法也逐渐发生了改变,本文主要介绍深度学习优化中局部最优相关的问题。
1. 低维度空间的局部最优
暂时先把深度学习的话题放到一边,回顾一个常见的数学知识:
- 函数在某个点的一阶导数等于0,且二阶导数小于0,则该点为局部极小值。
我们常常用以上知识来找到函数的极小值,但是函数可能同时具有多个局部极小值,哪一个才是全局极小值呢?
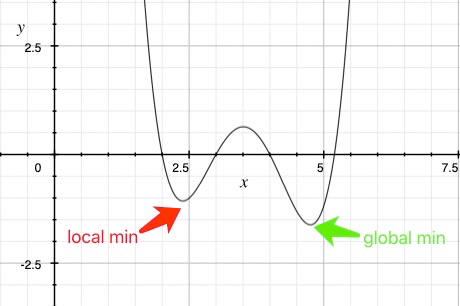
局部最优解问题是低维空间内常见的问题,所以凭借低维空间的经验,在深度学习优化过程中是否也存在类似的局部最优问题呢?
2. 高维度空间的局部最优
实际的深度学习应用场景中,模型的损失函数不大可能仅仅只与一到两个因子有关。一般情况下为了获得更好的效果,会尽可能的收集更多的因子。
举个例子,为了对房屋价格训练一个估价模型,仅有一个房屋面积因子是不够的。还会需要房屋所在省份,城市,房屋的房龄,与地铁的距离,附近的医院,学校,商场等等因子。如果将这些因子尽可能详尽的纳入考虑,映射为模型的特征输入,最终会得到成千上万维的特征。 设想一下,假设特征的维度是10000,该模型的损失函数存在10000个自变量。这样的高维损失函数无法在三维坐标系中画出来。如果这个损失函数上存在一阶导数为0的点,要使得这个点是局部最小值,那么需要这个点在10000个方向上的趋势都是向上弯曲。假设在每个方向向上弯曲向下弯曲的概率相同。 那么这个点是局部最小值的概率是\((0.5)^{10000}\) 这个概率过于小以至于我无法用小数点在这里表示,如果特征的维度进一步增加,这个概率还会进一步呈指数级下降。
所以,低维空间的直觉在高维空间不一定适用,在实际深度学习应用场景中出现局部最优点的概率非常低,更多情况下,一个一阶导数为0的点,在一些方向上的趋势是向上弯曲,而在另一些方向上的趋势是向下弯曲。这样的点我们称之为鞍点。
3. 鞍点
鞍点(Saddle point)这个名字非常形象,因为在三维空间的鞍点附近的曲面就像马鞍一样。
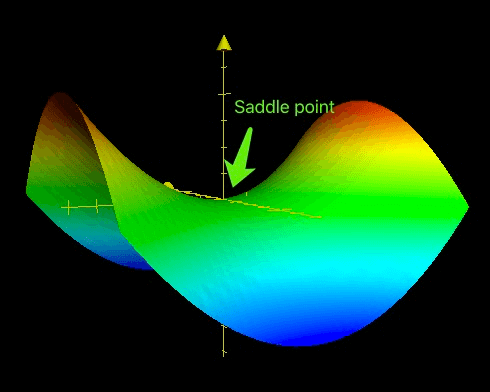
相比局部最优点,鞍点出现的概率很高,对深度学习训练过程造成的麻烦也大的多。鞍点附近的导数通常为0或接近于0,可能存在大量的平坦区域。
- 如果梯度计算集中在错误的方向,如上图中马鞍的纵向,会导致学习过程在鞍点附近震荡。
- 如果鞍点附近存在大量平坦区域,即使梯度计算选择了正确的方向,如上图中马鞍的横向,学习过程仍然会极其缓慢。
一些改进后的优化方法如Adam等,能够很好的缓解或者解决上述鞍点带来的问题,使梯度计算尽快走出鞍点。关于这些优化算法,我们将在单独的篇章讨论。